六、资料整理和计算
1.计算试件剪切极限平衡状态时的最大主应力σ1max
①根据应力环量表读数计算相应的轴向荷载P:
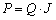
式中:K一压力环量表读数,格(0.01mm);
Q一应力环系数,kgf/格(即标定曲线的斜率)。 |
②计算轴向应变,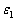
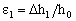
式中:△h1-一试件在某一瞬时的轴向总变形,cm;
h0试件的初始高度,cm。 |
③计算校正后面积s1;
鉴于试件横向变形很小,为简化计算,假定试件体积不变,每一瞬时可取一个纵向的平均截面,它的数值与横向均匀变形的横截面等量,如图4—14所示。由图4—14知,试件的瞬时高度hi=h1—△hi。
假定体积不变,Vo=Vi=sihi
为了减少计算工作,可将以上三项计算内容预先制成计算表以供查用。
④计算每一级瞬时荷载下的轴向应力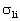
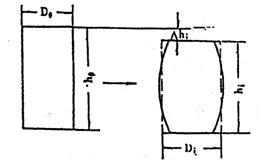 |
| 图4-14 试件变形示意图 |
在试验自始至终的一系列瞬时轴向主应力σ1i的数值中,接近试验最后阶段最大值σ1max,即应力应变(σ1i-ε1)曲线上的峰值,这就是试件处于剪切极限平衡状态时的最大主应力。每一组试件可获得一组对应的σ3-σ1max数值。
以上计算①一④均应填人记录表格内。
2.数解法求算C、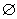 值 值
①将9个试件对应的σ3–σ1 (即σ1max,以下简写成σ1)值列入表格内。 |
